from fastcore.utils import *
from IPython.display import HTML,Markdown,display
from dialoghelper.stdtools import *
from fastcore.tools import *
import numpy as np, matplotlib.pyplot as plt, types, dataclasses, collections, time
import numpy as npI’d like to learn about chaos theory. In particular, I’ve heard that the logistic equation can be used to model population growth, and that it leads to “bifurcations”. I don’t understand. Can you walk me thru this gradually please
🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠
Great topic! The logistic equation is a wonderful gateway into chaos theory. Let’s build up to bifurcations step by step.
Starting point: Population growth
Imagine you’re modeling a population (say, rabbits). The simplest model says: next year’s population depends on this year’s population. If we call the population at time n as , we might write:
This is the logistic map. Here:
- is the population as a fraction of the maximum possible (so it’s between 0 and 1)
- is the “growth rate” parameter
- The term represents limited resources—as population grows, growth slows down
The key insight is: what happens over many generations depends dramatically on the value of r.
Before we go further, does this equation make intuitive sense to you? Can you see why:
- When is small, the population grows?
- When is close to 1, growth is suppressed?
Why is it called the “logistic map” please?
🧠🧠🧠🧠🧠🧠🧠🧠
Good question! The name comes from the French mathematician Pierre François Verhulst, who in the 1830s-40s developed the “logistic equation” to model population growth with limited resources.
The word “logistic” itself likely comes from the French logistique, related to logis (lodging/supplies). Verhulst may have chosen it to evoke the idea of “provisions” or “sustenance”—the limited resources that constrain population growth.
As for “map”—in mathematics, a map is just another word for a function that takes an input and produces an output. Since this equation maps one population value to the next value , we call it a map.
So “logistic map” = a function (map) based on Verhulst’s logistic growth model.
Ready to explore what happens when we iterate this map many times?
No, I’d like to build intuition first.
I get that would be a way to express growth, so that would represent 10% growth per unit time.
But What is the intuition behind the ? Just that as gets bigger (approaching the maximum of 1), then there should should be a factor that goes closer and closer to and therefore tends to limit growth?
🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠
Exactly right! You’ve got the core intuition.
The term represents environmental resistance—things like limited food, space, disease, predation. When the population is small (say ), this factor is large (0.9), so growth is mostly uninhibited. When population is near capacity (), the factor is small (0.1), severely limiting growth.
A nice way to think about it: the product is maximized when —medium-sized populations grow fastest. Too small and there aren’t enough individuals to reproduce; too large and resources run out.
One important thing to note: because we’re using the fraction of maximum capacity, the value of here isn’t quite like a simple percentage growth rate anymore. In this formulation, interesting dynamics happen when is between about 1 and 4. (If , the population can overshoot and go negative, which breaks the model!)
Do you want to try iterating the equation by hand for a few steps with a specific value, or would you prefer to write some code to see what happens over many generations?
First I just want to see what growth looks like. I am told that there are also “bifurcations” to understand, which I understand to be a way of talking about how overall behavior is different for different values of . But let me start gradually.
Please can you generate code for a dynamic chart in Altair, where I a slider can control the value of , and then I can see the chart showing how x changes from a small initial value of 0.05.
🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠
Here’s an interactive chart with a slider for :
import altair as alt
import pandas as pd
import numpy as np
# Generate data for different r values
def logistic_series(r, x0=0.05, n=50):
x = [x0]
for _ in range(n-1):
x.append(r * x[-1] * (1 - x[-1]))
return x
# Create data for a range of r values
data = []
for r in np.linspace(0.5, 4.0, 71): # r from 0.5 to 4.0 in steps of 0.05
xs = logistic_series(r)
for n, x in enumerate(xs):
data.append({'r': round(r, 2), 'n': n, 'x': x})
df = pd.DataFrame(data)
# Create slider
slider = alt.binding_range(min=0.5, max=4.0, step=0.05, name='r = ')
selection = alt.param('r_val', value=2.0, bind=slider)
# Chart
alt.Chart(df).mark_line(point=True).encode(
x=alt.X('n:Q', title='Generation'),
y=alt.Y('x:Q', title='Population (x)', scale=alt.Scale(domain=[0, 1])),
).add_params(selection).transform_filter(
alt.datum.r == selection
).properties(width=500, height=300, title='Logistic Map: Population over Time')Try sliding slowly from low values (like 1.0) up to higher values (like 3.5 and beyond). What patterns do you notice at different ranges of ?
def show_vega_chart_iframe(chart):
import base64
from IPython.display import HTML, IFrame
import base64
b64 = base64.b64encode(chart.to_html().encode()).decode()
return IFrame(src=f'data:text/html;base64,{b64}', width=600,height=400)import altair as alt
import pandas as pd
import numpy as np
# Generate data for different r values
def logistic_series(r, x0=0.05, n=50):
x = [x0]
for _ in range(n-1):
x.append(r * x[-1] * (1 - x[-1]))
return x
# Create data for a range of r values
data = []
for r in np.linspace(0.5, 4.0, 71): # r from 0.5 to 4.0 in steps of 0.05
xs = logistic_series(r)
for n, x in enumerate(xs):
data.append({'r': round(r, 2), 'n': n, 'x': x})
df = pd.DataFrame(data)
# Create slider
slider = alt.binding_range(min=0.5, max=4.0, step=0.05, name='r = ')
selection = alt.param('r_val', value=2.0, bind=slider)
# Chart
c = alt.Chart(df).mark_line(point=True).encode(
x=alt.X('n:Q', title='Generation'),
y=alt.Y('x:Q', title='Population (x)', scale=alt.Scale(domain=[0, 1])),
).add_params(selection).transform_filter(
alt.datum.r == selection
).properties(width=500, height=300, title='Logistic Map: Population over Time')show_vega_chart_iframe(c)Okay. Let’s study the bifurcations. So I am going to want on the left-right axis I suppose, and then on the vertical axis I guess I want … what?
🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠
Great question! Think about it this way: at r = 3.5, your chart shows the population bouncing between 4 distinct values (roughly 0.38, 0.50, 0.83, 0.87).
So on the vertical axis, you want to plot the values that x settles into after the initial transient dies out.
For each r value, you’d:
- Run the iteration many times to let it “settle”
- Record the last several x values it visits
- Plot those as points at that r
For r = 2.5, you’d see just 1 point (stable fixed point). For r = 3.5, you’d see 4 points. For r = 3.9, you’d see a chaotic scatter of points.
Does that make sense? Want to try coding it?
Note: Some earlier messages were removed due to context limits—there were originally 11 messages, now 5. Let me know if you need me to recap anything.
import matplotlib.pyplot as plt
import numpy as np
r_values = np.linspace(2.5, 4.0, 1000)
iterations = 1000
last = 100 # keep last 100 values
plt.figure(figsize=(12, 8))
for r in r_values:
x = 0.5
for _ in range(iterations - last):
x = r * x * (1 - x) # discard transient
xs = []
for _ in range(last):
x = r * x * (1 - x)
xs.append(x)
plt.plot([r] * last, xs, 'k,', markersize=0.5)
plt.xlabel('r')
plt.ylabel('x (stable values)')
plt.title('Bifurcation Diagram of the Logistic Map')
plt.show()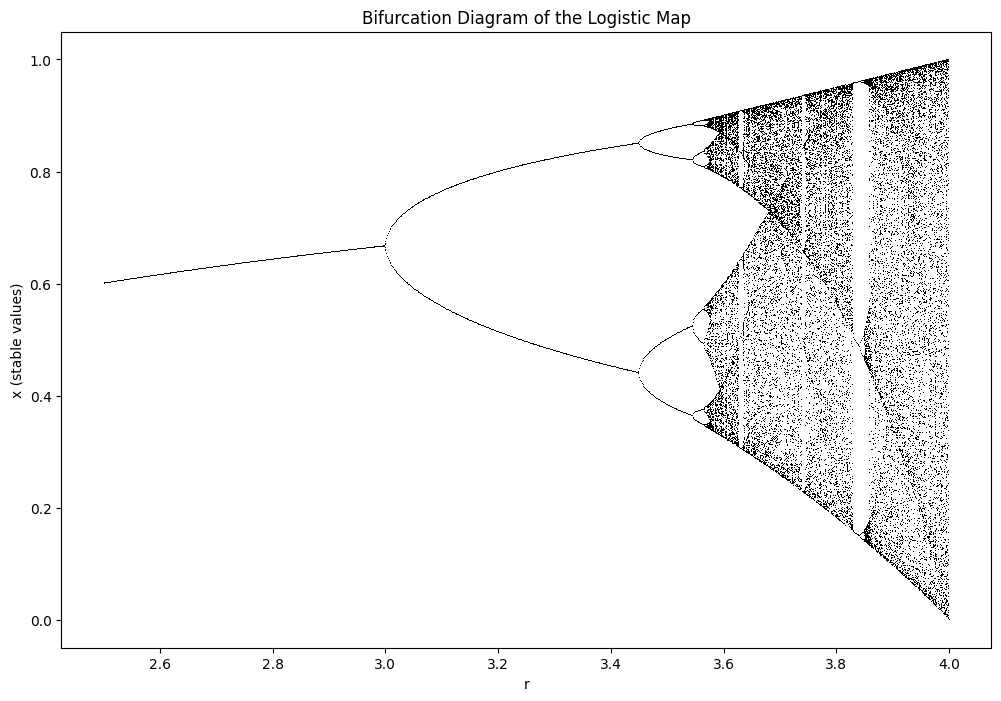
Does anyone know why there is that vertical empty region around roughly, where the number of stable values suddenly goes down again to 3 after apparently being much higher?
🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠
That’s a wonderful observation! That’s called a periodic window (or “island of stability”).
Around r ≈ 3.83, something special happens: a stable period-3 cycle appears. The system, which was chaotic, suddenly settles into bouncing between just 3 values!
This is actually famous in mathematics. Li and Yorke wrote a paper called “Period Three Implies Chaos” (1975) showing that if a system has a period-3 cycle, it must also have cycles of every other period—a hallmark of chaos.
If you zoom in on that window, you’d see it has the same bifurcation structure as the whole diagram—it splits into 6, then 12, etc., before going chaotic again. This self-similarity repeats at every scale!
Would you like to zoom into that region to see the structure more clearly?
Context note: Some earlier messages were removed due to context limits—originally 14 messages, now 8.
Interactive Bifurcation Explorer
Is there a way to use Vega/Altair to make the above chart zoomable? it seems like a tricky problem, because there’s too much data to precompute all of it, so presumably it would be necessary to recompute every time the zoom region is finalized.
🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠
Unfortunately, pure Altair/Vega isn’t well-suited for this. It’s declarative—the data is baked into the spec sent to the browser, with no way to call Python when zoom changes.
Better options for dynamic recomputation:
- ipywidgets + matplotlib — simplest; use sliders to control the r range, recompute on change
- Panel + HoloViews — supports dynamic ranges with Python callbacks
- Bokeh — can do Python callbacks on zoom events
Want to try the ipywidgets approach? It would give you two sliders (r_min, r_max) that recompute and redraw the bifurcation diagram for that region.
I’d really prefer to do it all in JS so that I can host this on a static site.
🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠
That’s a great approach! Here’s a self-contained HTML file with a Canvas-based zoomable bifurcation diagram:
Logistic Map Bifurcation Diagram
Click and drag to zoom into a region
You can save this as an HTML file and open it directly in a browser. Click and drag to zoom into any region—it recomputes the diagram in JS each time.
That looks promising but I’ll need it an iframe in order to render it in the notebook nondestructively, please.
🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠🧠
from IPython.display import IFrame
import base64
html = '''<!DOCTYPE html>
<html>
<head>
<style>
body { font-family: sans-serif; margin: 10px; }
canvas { border: 1px solid #ccc; cursor: crosshair; }
.controls { margin: 10px 0; }
button { margin-right: 10px; padding: 5px 15px; }
</style>
</head>
<body>
<h4>Logistic Map Bifurcation Diagram</h4>
<div class="controls">
<button onclick="resetZoom()">Reset Zoom</button>
<span id="info">r: [2.5, 4.0], x: [0, 1]</span>
</div>
<canvas id="canvas" width="700" height="450"></canvas>
<p>Click and drag to zoom into a region</p>
<script>
const canvas = document.getElementById('canvas'), ctx = canvas.getContext('2d'), info = document.getElementById('info')
let rMin = 2.5, rMax = 4.0, xMin = 0, xMax = 1, selecting = false, selStart = null, selEnd = null
function draw() {
ctx.fillStyle = 'white'
ctx.fillRect(0, 0, canvas.width, canvas.height)
ctx.fillStyle = 'rgba(0,0,0,0.3)'
const rSteps = canvas.width * 2, iters = 1000, last = 100
for (let i = 0; i < rSteps; i++) {
const r = rMin + (rMax - rMin) * i / rSteps
let x = 0.5
for (let j = 0; j < iters - last; j++) x = r * x * (1 - x)
for (let j = 0; j < last; j++) {
x = r * x * (1 - x)
if (x >= xMin && x <= xMax) {
const px = (r - rMin) / (rMax - rMin) * canvas.width
const py = canvas.height - (x - xMin) / (xMax - xMin) * canvas.height
ctx.fillRect(px, py, 1, 1)
}
}
}
info.textContent = `r: [${rMin.toFixed(4)}, ${rMax.toFixed(4)}], x: [${xMin.toFixed(4)}, ${xMax.toFixed(4)}]`
}
function toCoords(e) {
const rect = canvas.getBoundingClientRect()
const px = e.clientX - rect.left, py = e.clientY - rect.top
return { r: rMin + (rMax - rMin) * px / canvas.width, x: xMax - (xMax - xMin) * py / canvas.height }
}
canvas.onmousedown = e => { selecting = true; selStart = toCoords(e); selEnd = selStart }
canvas.onmousemove = e => {
if (!selecting) return
selEnd = toCoords(e)
draw()
const x1 = (selStart.r - rMin) / (rMax - rMin) * canvas.width
const y1 = canvas.height - (selStart.x - xMin) / (xMax - xMin) * canvas.height
const x2 = (selEnd.r - rMin) / (rMax - rMin) * canvas.width
const y2 = canvas.height - (selEnd.x - xMin) / (xMax - xMin) * canvas.height
ctx.strokeStyle = 'blue'
ctx.strokeRect(Math.min(x1,x2), Math.min(y1,y2), Math.abs(x2-x1), Math.abs(y2-y1))
}
canvas.onmouseup = e => {
if (!selecting) return
selecting = false
selEnd = toCoords(e)
const newRMin = Math.min(selStart.r, selEnd.r), newRMax = Math.max(selStart.r, selEnd.r)
const newXMin = Math.min(selStart.x, selEnd.x), newXMax = Math.max(selStart.x, selEnd.x)
if (newRMax - newRMin > 0.01 && newXMax - newXMin > 0.01) { rMin = newRMin; rMax = newRMax; xMin = newXMin; xMax = newXMax; draw() }
}
function resetZoom() { rMin = 2.5; rMax = 4.0; xMin = 0; xMax = 1; draw() }
draw()
</script>
</body>
</html>'''
IFrame(src=f'data:text/html;base64,{base64.b64encode(html.encode()).decode()}', width=750, height=580)from IPython.display import IFrame
import base64
html = '''<!DOCTYPE html>
<html>
<head>
<style>
body { font-family: sans-serif; margin: 10px; }
canvas { border: 1px solid #ccc; cursor: crosshair; }
.controls { margin: 10px 0; }
button { margin-right: 10px; padding: 5px 15px; }
</style>
</head>
<body>
<h4>Logistic Map Bifurcation Diagram</h4>
<div class="controls">
<button onclick="resetZoom()">Reset Zoom</button>
<span id="info">r: [2.5, 4.0], x: [0, 1]</span>
</div>
<canvas id="canvas" width="700" height="450"></canvas>
<p>Click and drag to zoom into a region</p>
<script>
const canvas = document.getElementById('canvas'), ctx = canvas.getContext('2d'), info = document.getElementById('info')
let rMin = 2.5, rMax = 4.0, xMin = 0, xMax = 1, selecting = false, selStart = null, selEnd = null
function draw() {
ctx.fillStyle = 'white'
ctx.fillRect(0, 0, canvas.width, canvas.height)
ctx.fillStyle = 'rgba(0,0,0,0.3)'
const rSteps = canvas.width * 2, iters = 1000, last = 100
for (let i = 0; i < rSteps; i++) {
const r = rMin + (rMax - rMin) * i / rSteps
let x = 0.5
for (let j = 0; j < iters - last; j++) x = r * x * (1 - x)
for (let j = 0; j < last; j++) {
x = r * x * (1 - x)
if (x >= xMin && x <= xMax) {
const px = (r - rMin) / (rMax - rMin) * canvas.width
const py = canvas.height - (x - xMin) / (xMax - xMin) * canvas.height
ctx.fillRect(px, py, 1, 1)
}
}
}
info.textContent = `r: [${rMin.toFixed(4)}, ${rMax.toFixed(4)}], x: [${xMin.toFixed(4)}, ${xMax.toFixed(4)}]`
}
function toCoords(e) {
const rect = canvas.getBoundingClientRect()
const px = e.clientX - rect.left, py = e.clientY - rect.top
return { r: rMin + (rMax - rMin) * px / canvas.width, x: xMax - (xMax - xMin) * py / canvas.height }
}
canvas.onmousedown = e => { selecting = true; selStart = toCoords(e); selEnd = selStart }
canvas.onmousemove = e => {
if (!selecting) return
selEnd = toCoords(e)
draw()
const x1 = (selStart.r - rMin) / (rMax - rMin) * canvas.width
const y1 = canvas.height - (selStart.x - xMin) / (xMax - xMin) * canvas.height
const x2 = (selEnd.r - rMin) / (rMax - rMin) * canvas.width
const y2 = canvas.height - (selEnd.x - xMin) / (xMax - xMin) * canvas.height
ctx.strokeStyle = 'blue'
ctx.strokeRect(Math.min(x1,x2), Math.min(y1,y2), Math.abs(x2-x1), Math.abs(y2-y1))
}
canvas.onmouseup = e => {
if (!selecting) return
selecting = false
selEnd = toCoords(e)
const newRMin = Math.min(selStart.r, selEnd.r), newRMax = Math.max(selStart.r, selEnd.r)
const newXMin = Math.min(selStart.x, selEnd.x), newXMax = Math.max(selStart.x, selEnd.x)
if (newRMax - newRMin > 0.01 && newXMax - newXMin > 0.01) { rMin = newRMin; rMax = newRMax; xMin = newXMin; xMax = newXMax; draw() }
}
function resetZoom() { rMin = 2.5; rMax = 4.0; xMin = 0; xMax = 1; draw() }
draw()
</script>
</body>
</html>'''
IFrame(src=f'data:text/html;base64,{base64.b64encode(html.encode()).decode()}', width=750, height=580)